al_10 图

阅读数: 次 2021-01-03

如需转载，请根据 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议许可，附上本文作者及链接。
本文作者： 执笔成念
作者昵称： zbcn
本文链接： https://1363653611.github.io/zbcn.github.io/2021/01/03/al_10%E5%9B%BE/

图

基本概念

线性表和树两类数据结构，线性表中的元素是“一对一”的关系，树中的元素是“一对多”的关系
图结构中的元素则是“多对多”的关系
图（Graph）是一种复杂的非线性结构，在图结构中，每个元素都可以有零个或多个前驱，也可以有零个或多个后继，也就是说，元素之间的关系是任意的。

无向图

无向图是由顶点和边构成。

有向图

有向图是由顶点和有向边构成。

完全图

如果任意两个顶点之间都存在边叫完全图，有向的边叫有向完全图。如果无重复的边或者顶点到自身的边叫简单图。

图的节点表示

@Data
   static class GraphNode<T> {
       T data;
       List<GraphNode<T>> neighborList;
       boolean visited;

       public GraphNode(T data) {
           this.data = data;
           this.neighborList = Lists.newArrayList();
           this.visited = false;
       }

       public boolean equals(GraphNode<T> node) {
           return this.data.equals(node.data);
       }

       /**
        * 还原图中所有节点为未访问
        */
       public void restoreVisited() {
           restoreVisited(this);
       }

       /**
        * 还原node的图所有节点为未访问
        * @param node
        */
       private void restoreVisited(GraphNode<T> node) {
           if (node.visited) {
               node.visited = false;
           }
           List<GraphNode<T>> neighbors = node.neighborList;
           for (int i = 0; i < neighbors.size(); i++) {
               restoreVisited(neighbors.get(i));
           }
       }
   }

图的深度优先和广度优先搜索

图的深度优先搜索 DFS (Depth First Search)

概述

图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。

思路：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。显然，深度优先搜索是一个递归的过程。

无向图深度优先搜索图解

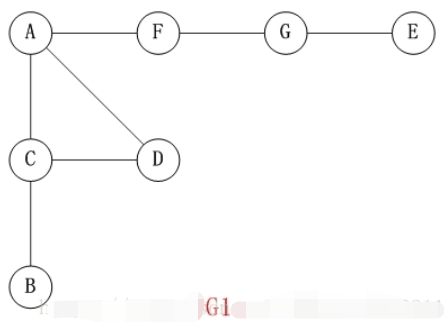
对上面的图G1进行深度优先遍历，从顶点A开始。

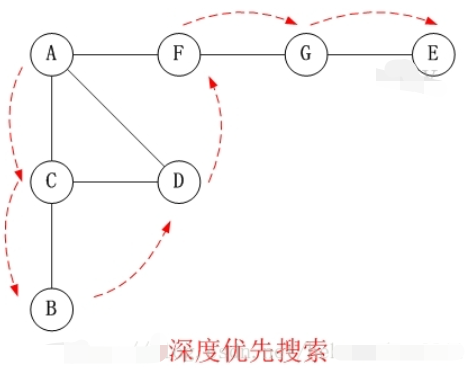
说明

第1步：访问A。
第2步：访问(A的邻接点)C。在第1步访问A之后，接下来应该访问的是A的邻接点，即”C,D,F”中的一个。但在本文的实现中，顶点ABCDEFG是按照顺序存储，C在”D和F”的前面，因此，先访问C。
第3步：访问(C的邻接点)B。在第2步访问C之后，接下来应该访问C的邻接点，即”B和D”中一个(A已经被访问过，就不算在内)。而由于B在D之前，先访问B。
第4步：访问(C的邻接点)D。
第5步：访问(A的邻接点)F。
第6步：访问(F的邻接点)G。
第7步：访问(G的邻接点)E。

访问顺序是：A -> C -> B -> D -> F -> G -> E

有向图深度优先搜索图解

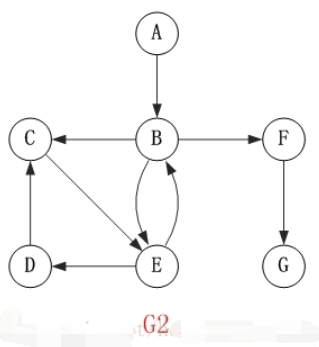
对上面的图G2进行深度优先遍历，从顶点A开始。

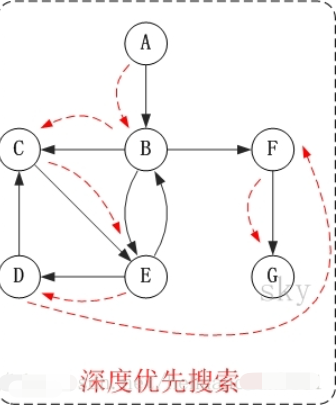
访问顺序是：A -> B -> C -> E -> D -> F -> G

广度优先 BFS (Breadth-First-Search)

介绍

从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远。

无向图广度优先搜索图解

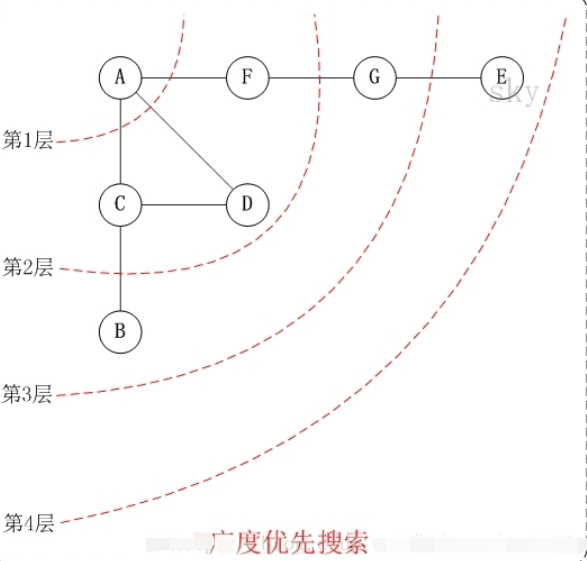
访问顺序是：A -> C -> D -> F -> B -> G -> E

有向图广度优先搜索图解

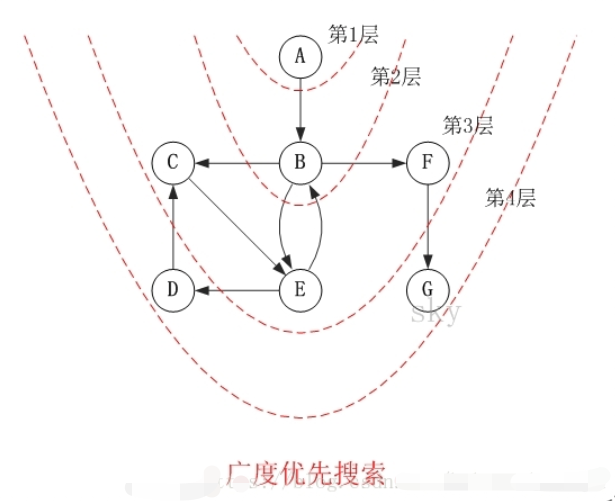
访问顺序是：A -> B -> C -> E -> F -> D -> G

代码实现

/**
 * 图的广度优先搜索和深度优先搜索实现
 * <br/>
 *
 * @author zbcn8
 * @since 2021/1/27 11:40
 */
public class GraphSearch<T> {

    private static StringBuffer searchPathDFS = new StringBuffer();

    private static StringBuffer searchPathBFS = new StringBuffer();


    /**
     * 深度有限搜索法
     * @param root
     */
    public void searchDFS(GraphNode<T> root){
        if (root == null){
            return;
        }
        if (searchPathDFS.length() > 0){
            searchPathDFS.append("->");
        }
        searchPathDFS.append(root.data.toString());
        root.visited = true;
        for (GraphNode<T> node :root.neighborList){
            if (!node.visited){
                searchDFS(node);
            }
        }
    }

    /**
     * 广度优先搜索实现,使用队列
     * @param root
     */
    public void searchBFS(GraphNode<T> root){
        Deque<GraphNode<T>> queue = new ArrayDeque<>();
        if(searchPathBFS.length() > 0){
            searchPathBFS.append("->");
        }
        searchPathBFS.append(root.data.toString());
        root.visited = true;
        // 添加到队尾
        queue.addLast(root);
        while (!queue.isEmpty()){
            GraphNode<T> r = queue.pollLast();
            for (GraphNode<T> node : r.neighborList) {
                if(!node.visited){
                    searchPathBFS.append("->");
                    searchPathBFS.append(node.data.toString());
                    node.visited = true;
                    queue.addLast(node);
                }
            }
        }
    }

    @Data
    static class GraphNode<T> {
        T data;
        List<GraphNode<T>> neighborList;
        boolean visited;

        public GraphNode(T data) {
            this.data = data;
            this.neighborList = Lists.newArrayList();
            this.visited = false;
        }

        public boolean equals(GraphNode<T> node) {
            return this.data.equals(node.data);
        }

        /**
         * 还原图中所有节点为未访问
         */
        public void restoreVisited() {
            restoreVisited(this);
        }

        /**
         * 还原node的图所有节点为未访问
         * @param node
         */
        private void restoreVisited(GraphNode<T> node) {
            if (node.visited) {
                node.visited = false;
            }
            List<GraphNode<T>> neighbors = node.neighborList;
            for (int i = 0; i < neighbors.size(); i++) {
                restoreVisited(neighbors.get(i));
            }
        }
    }

    static GraphNode<Integer> node1;
    static GraphNode<Integer> node2;
    static GraphNode<Integer> node3;
    static GraphNode<Integer> node4;
    static GraphNode<Integer> node5;
    static GraphNode<Integer> node6;
    static GraphNode<Integer> node7;
    static GraphNode<Integer> node8;
    static GraphNode<Integer> node9;
    static GraphNode<Integer> node10;

    public static void main(String[] args) {
        buildGraph();
//        GraphSearch<Integer> graphSearch = new GraphSearch<Integer>();
//        graphSearch.searchDFS(node1);
//        System.out.println(searchPathDFS.toString());

        GraphSearch<Integer> graphSearchBFS = new GraphSearch<Integer>();
        graphSearchBFS.searchBFS(node1);
        System.out.println(searchPathBFS.toString());
    }

    private static void buildGraph() {

        node1 = new GraphNode<Integer>(1);
        node2 = new GraphNode<Integer>(2);
        node3 = new GraphNode<Integer>(3);
        node4 = new GraphNode<Integer>(4);
        node5 = new GraphNode<Integer>(5);
        node6 = new GraphNode<Integer>(6);
        node7 = new GraphNode<Integer>(7);
        node8 = new GraphNode<Integer>(8);
        node9 = new GraphNode<Integer>(9);
        node10 = new GraphNode<Integer>(10);

        node1.neighborList.add(node2);
        node1.neighborList.add(node3);

        node2.neighborList.add(node4);
        node2.neighborList.add(node5);
        node2.neighborList.add(node6);

        node3.neighborList.add(node1);
        node3.neighborList.add(node6);
        node3.neighborList.add(node7);
        node3.neighborList.add(node8);

        node4.neighborList.add(node2);
        node4.neighborList.add(node5);

        node5.neighborList.add(node2);
        node5.neighborList.add(node4);
        node5.neighborList.add(node6);

        node6.neighborList.add(node2);
        node6.neighborList.add(node5);
        node6.neighborList.add(node3);
        node6.neighborList.add(node8);
        node6.neighborList.add(node9);
        node6.neighborList.add(node10);

        node7.neighborList.add(node3);

        node8.neighborList.add(node3);
        node8.neighborList.add(node6);
        node8.neighborList.add(node9);

        node9.neighborList.add(node6);
        node9.neighborList.add(node8);
        node9.neighborList.add(node10);

        node10.neighborList.add(node6);
        node10.neighborList.add(node9);
    }


}

1	/**
2	* 图的广度优先搜索和深度优先搜索实现
3	* <br/>
4	*
5	* @author zbcn8
6	* @since 2021/1/27 11:40
7	*/
8	public class GraphSearch<T> {
9
10	private static StringBuffer searchPathDFS = new StringBuffer();
11
12	private static StringBuffer searchPathBFS = new StringBuffer();
13
14
15	/**
16	* 深度有限搜索法
17	* @param root
18	*/
19	public void searchDFS(GraphNode<T> root){
20	if (root == null){
21	return;
22	}
23	if (searchPathDFS.length() > 0){
24	searchPathDFS.append("->");
25	}
26	searchPathDFS.append(root.data.toString());
27	root.visited = true;
28	for (GraphNode<T> node :root.neighborList){
29	if (!node.visited){
30	searchDFS(node);
31	}
32	}
33	}
34
35	/**
36	* 广度优先搜索实现,使用队列
37	* @param root
38	*/
39	public void searchBFS(GraphNode<T> root){
40	Deque<GraphNode<T>> queue = new ArrayDeque<>();
41	if(searchPathBFS.length() > 0){
42	searchPathBFS.append("->");
43	}
44	searchPathBFS.append(root.data.toString());
45	root.visited = true;
46	// 添加到队尾
47	queue.addLast(root);
48	while (!queue.isEmpty()){
49	GraphNode<T> r = queue.pollLast();
50	for (GraphNode<T> node : r.neighborList) {
51	if(!node.visited){
52	searchPathBFS.append("->");
53	searchPathBFS.append(node.data.toString());
54	node.visited = true;
55	queue.addLast(node);
56	}
57	}
58	}
59	}
60
61	@Data
62	static class GraphNode<T> {
63	T data;
64	List<GraphNode<T>> neighborList;
65	boolean visited;
66
67	public GraphNode(T data) {
68	this.data = data;
69	this.neighborList = Lists.newArrayList();
70	this.visited = false;
71	}
72
73	public boolean equals(GraphNode<T> node) {
74	return this.data.equals(node.data);
75	}
76
77	/**
78	* 还原图中所有节点为未访问
79	*/
80	public void restoreVisited() {
81	restoreVisited(this);
82	}
83
84	/**
85	* 还原node的图所有节点为未访问
86	* @param node
87	*/
88	private void restoreVisited(GraphNode<T> node) {
89	if (node.visited) {
90	node.visited = false;
91	}
92	List<GraphNode<T>> neighbors = node.neighborList;
93	for (int i = 0; i < neighbors.size(); i++) {
94	restoreVisited(neighbors.get(i));
95	}
96	}
97	}
98
99	static GraphNode<Integer> node1;
100	static GraphNode<Integer> node2;
101	static GraphNode<Integer> node3;
102	static GraphNode<Integer> node4;
103	static GraphNode<Integer> node5;
104	static GraphNode<Integer> node6;
105	static GraphNode<Integer> node7;
106	static GraphNode<Integer> node8;
107	static GraphNode<Integer> node9;
108	static GraphNode<Integer> node10;
109
110	public static void main(String[] args) {
111	buildGraph();
112	// GraphSearch<Integer> graphSearch = new GraphSearch<Integer>();
113	// graphSearch.searchDFS(node1);
114	// System.out.println(searchPathDFS.toString());
115
116	GraphSearch<Integer> graphSearchBFS = new GraphSearch<Integer>();
117	graphSearchBFS.searchBFS(node1);
118	System.out.println(searchPathBFS.toString());
119	}
120
121	private static void buildGraph() {
122
123	node1 = new GraphNode<Integer>(1);
124	node2 = new GraphNode<Integer>(2);
125	node3 = new GraphNode<Integer>(3);
126	node4 = new GraphNode<Integer>(4);
127	node5 = new GraphNode<Integer>(5);
128	node6 = new GraphNode<Integer>(6);
129	node7 = new GraphNode<Integer>(7);
130	node8 = new GraphNode<Integer>(8);
131	node9 = new GraphNode<Integer>(9);
132	node10 = new GraphNode<Integer>(10);
133
134	node1.neighborList.add(node2);
135	node1.neighborList.add(node3);
136
137	node2.neighborList.add(node4);
138	node2.neighborList.add(node5);
139	node2.neighborList.add(node6);
140
141	node3.neighborList.add(node1);
142	node3.neighborList.add(node6);
143	node3.neighborList.add(node7);
144	node3.neighborList.add(node8);
145
146	node4.neighborList.add(node2);
147	node4.neighborList.add(node5);
148
149	node5.neighborList.add(node2);
150	node5.neighborList.add(node4);
151	node5.neighborList.add(node6);
152
153	node6.neighborList.add(node2);
154	node6.neighborList.add(node5);
155	node6.neighborList.add(node3);
156	node6.neighborList.add(node8);
157	node6.neighborList.add(node9);
158	node6.neighborList.add(node10);
159
160	node7.neighborList.add(node3);
161
162	node8.neighborList.add(node3);
163	node8.neighborList.add(node6);
164	node8.neighborList.add(node9);
165
166	node9.neighborList.add(node6);
167	node9.neighborList.add(node8);
168	node9.neighborList.add(node10);
169
170	node10.neighborList.add(node6);
171	node10.neighborList.add(node9);
172	}
173
174
175	}

图