如需转载,请根据 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 许可,附上本文作者及链接。
本文作者: 执笔成念
作者昵称: zbcn
本文链接: https://1363653611.github.io/zbcn.github.io/2020/06/21/al_05_%E5%B9%B3%E8%A1%A1%E4%BA%8C%E5%8F%89%E6%A0%91/
平衡二叉树的由来
平衡二叉树存在缺馅
- 二叉搜索树一定程度上可以提高搜索效率,但是当原序列有序时,例如序列 A = {1,2,3,4,5,6},构造二叉搜索树如图 1.1。依据此序列构造的二叉搜索树为右斜树,同时二叉树退化成单链表,搜索效率降低为 O(n)。
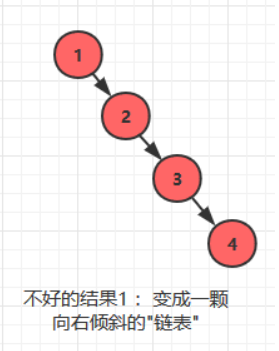
- 插入和删除操作可能降低未来操作的性能
什么是平衡二叉树
Balanced BinaryTree 平衡二叉树,又被称作VAL 树.特点:为一颗空树,或者它的左右两颗子树之前的高度差的绝对值不能超过1,并且左右两颗子树都是一颗平衡二叉树.
平衡二叉树一般是一个有序树,它具有二叉树的所有性质,其遍历操作和二叉树的遍历操作相同。但是由于其对二叉树施加了额外限制,因而其添加、删除操作都必须保证平衡二叉树的因子被保持。
平衡因子
指的是该节点的两个子树,即左子树和右子树的高度差.即用左子树的高度减去右子树的高度,如果该节点的某个子树不存在,则该子树的高度为0,如果高度差的绝对值超过1就要根据情况进行调整。
下图中:
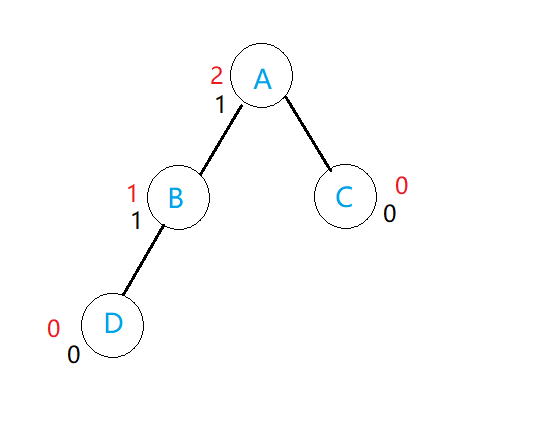
- 对根结点A而言, 它左子树高度为2, 右子树高度为1, 那么它的平衡因子BF = 2 - 1 = 1
- 对结点B而言, 它左子树高度为1, 没有右子树(高度视为0),BF = 1 - 0 = 1;
平衡二叉树的节点
1 | /** |
2 | * 平衡二叉树的节点 |
3 | * <br/> |
4 | * @author zbcn8 |
5 | * @since 2020/8/19 13:32 |
6 | */ |
7 | public static class Node<T>{ |
8 | |
9 | /** |
10 | * 节点值 |
11 | */ |
12 | private T val; |
13 | |
14 | /** |
15 | * 深度,这里计算每个结点的深度,通过深度的比较可得出是否平衡 |
16 | */ |
17 | private int depth; |
18 | |
19 | /** |
20 | * 父节点 |
21 | */ |
22 | private Node<T> parent; |
23 | |
24 | /** |
25 | * 左子树 |
26 | */ |
27 | private Node<T> left; |
28 | |
29 | /** |
30 | * 右子树 |
31 | */ |
32 | private Node<T> right; |
33 | |
34 | public Node(T val) { |
35 | this.val = val; |
36 | depth=0; |
37 | parent=null; |
38 | left= null; |
39 | right = null; |
40 | |
41 | } |
42 | } |
平衡因子
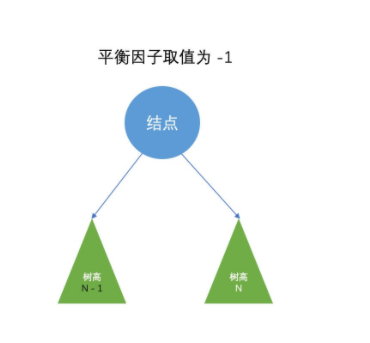
某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子(BF,Balance Factor)。平衡二叉树中不存在平衡因子大于 1 的节点,在一棵平衡二叉树中,节点的平衡因子只能取 0 (左右子树等高)、1(左子树比较高) 或者 -1(右子树比较高) ,分别对应着。
- 左右子树等高
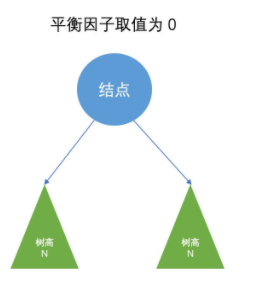
- 左子树高
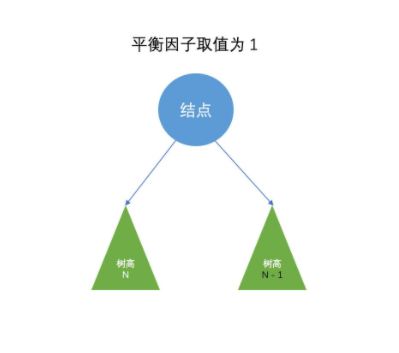
- 右子树高
最小失衡子树
在新插入的结点向上查找,以第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树。也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
如下图:
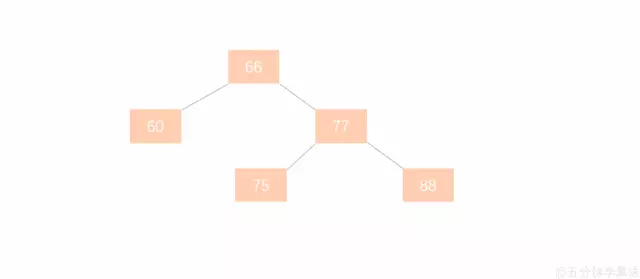
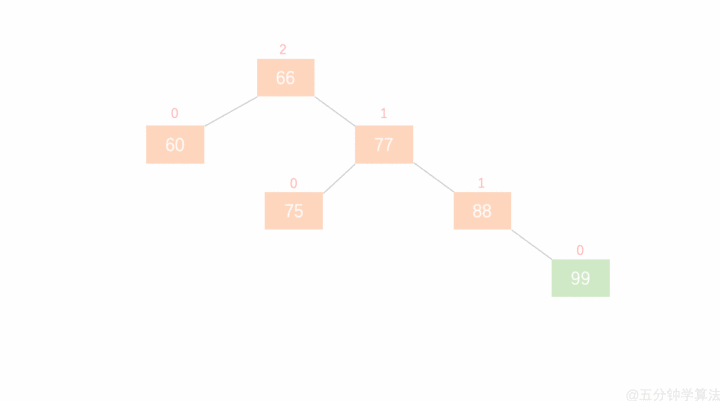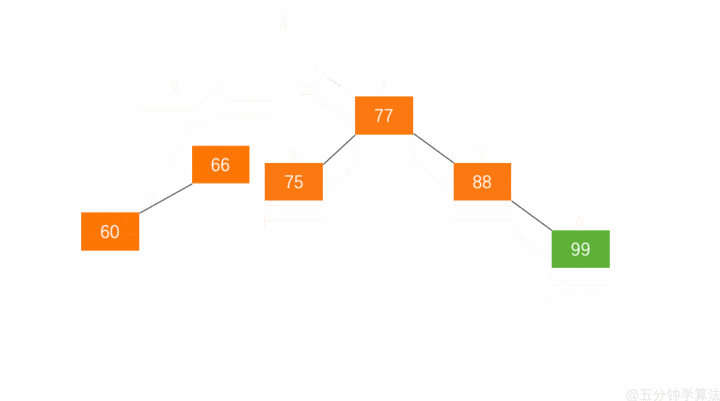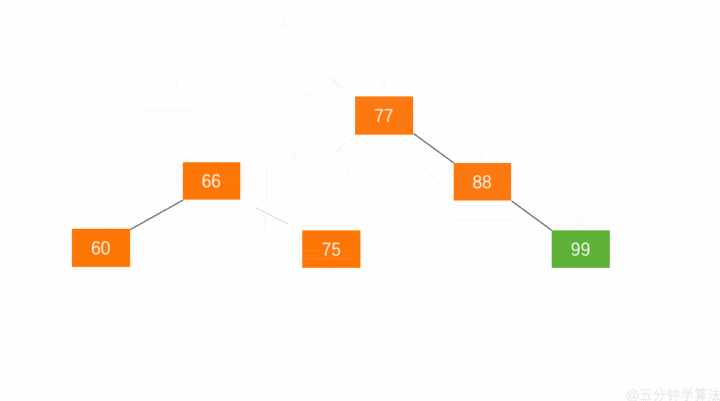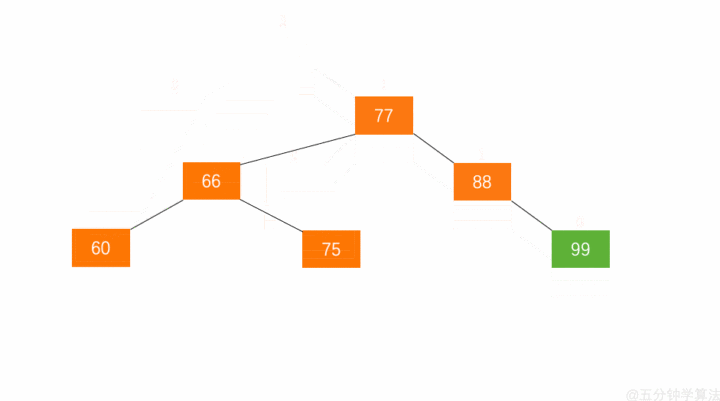
上图中,增加99节点后,节点 66 的左子树高度为 1,右子树高度为 3,此时平衡因子为 -2,树失去平衡。
二叉树的修正机制
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式,左旋 与 右旋 。
左旋
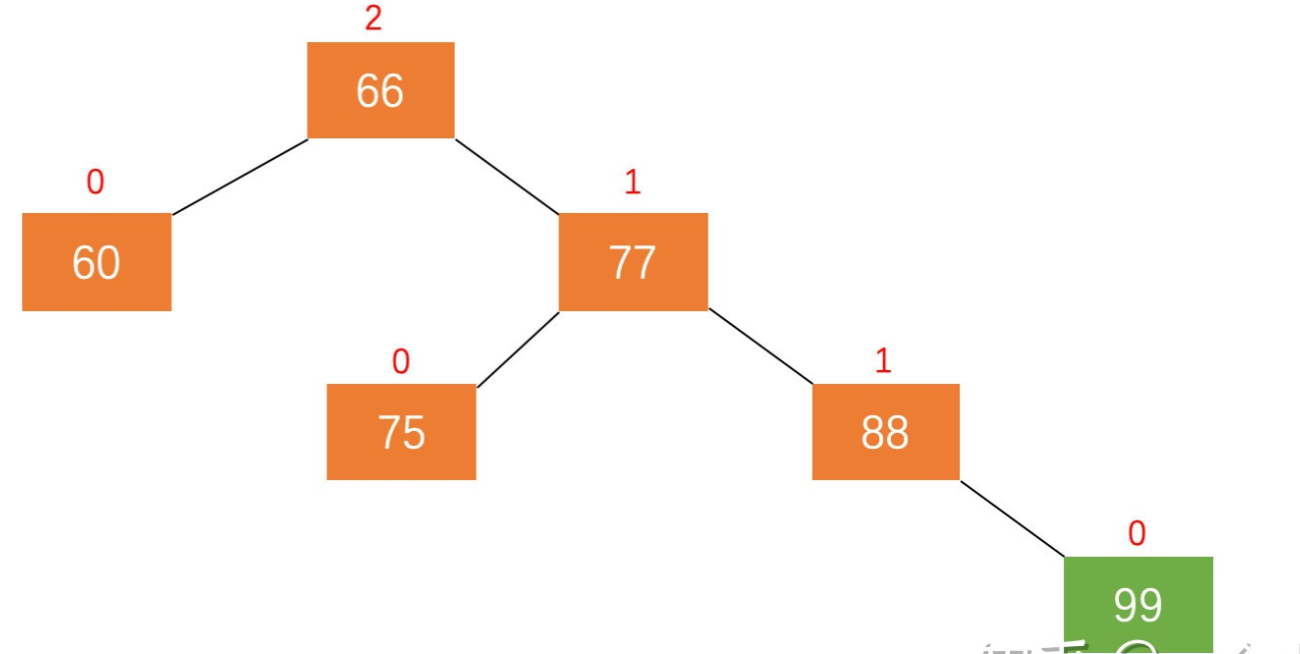
上图中:加入新节点 99 后, 节点 66 的左子树高度为 1,右子树高度为 3,此时平衡因子为 -2。为保证树的平衡,此时需要对节点 66 做出旋转,因为右子树高度高于左子树,对节点进行左旋操作。
操作流程如下:
- 节点的右孩子替代此节点位置
- 右孩子的左子树变为该节点的右子树
- 节点本身变为右孩子的左子树
如下图:
右旋
右旋操作与左旋类似,
操作流程为
- 节点的左孩子代表此节点
- 节点的左孩子的右子树变为节点的左子树
- 将此节点作为左孩子节点的右子树。
如下图:
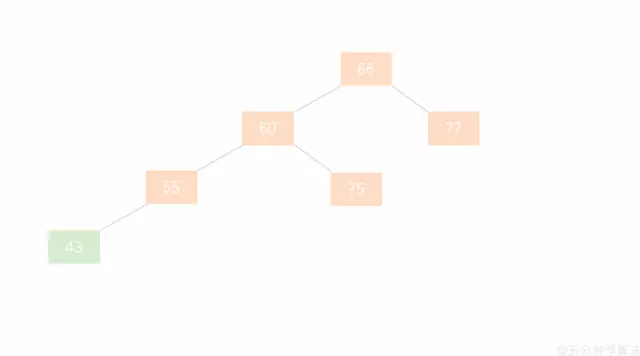
四种失衡的情况
| 插入方式 | 描述 | 旋转方式 |
|---|---|---|
| LL | 在 A 的左子树根节点的左子树上插入节点而破坏平衡 | 右旋转 |
| RR | 在 A 的右子树根节点的右子树上插入节点而破坏平衡 | 左旋转 |
| LR | 在A的左子树根节点的右子树上插入节点而破坏平衡 | 先左旋后右旋 |
| RL | 在 A 的右子树根节点的左子树上插入节点而破坏平衡 | 先右旋后左旋 |
| RL | 在 A 的右子树根节点的左子树上插入节点而破坏平衡 | 先右旋后左旋 |
LL型 -(左孩子的左子树)通过右旋解决
在结点的左孩子的左子树中插入数据。

代码
1 | /** |
2 | * 右旋 |
3 | * @param node |
4 | * @return |
5 | */ |
6 | public Node<T> rotateRight(Node<T> node){ |
7 | //获取左儿子 |
8 | Node<T> left = node.getLeft(); |
9 | //将左儿子的右儿子("拖油瓶"结点)链接到旋转后的node的左链接中 |
10 | node.setLeft(left.getRight()); |
11 | // 调转node和它左儿子的父子关系,使node成为它原左儿子的右子树 |
12 | left.setRight(node); |
13 | // 更新并维护受影响结点的height |
14 | node.setHeight(max(height(node.getLeft()), height(node.getRight()))+1); |
15 | // 更新并维护受影响结点的height |
16 | left.setHeight(max(height(left.getLeft()),height(left.getRight()))+1); |
17 | return left; |
18 | } |
RR型-(右孩子的右子树)通过左旋解决
只需要执行一次左旋即可。
代码
1 | /** |
2 | * 左旋 |
3 | * @param node |
4 | * @return |
5 | */ |
6 | public Node<T> rotateLeft(Node<T> node){ |
7 | //获取右儿子 |
8 | Node<T> right = node.getRight(); |
9 | //将右儿子的左儿子("拖油瓶"结点)链接到旋转后的node的右侧链接中 |
10 | node.setRight(right.getLeft()); |
11 | //调转node 节点和它右侧儿子的父子关系,使node 成为它原右生儿子的左子树 |
12 | right.setLeft(node); |
13 | node.setHeight(max(height(node.getRight()),height(node.getLeft()))+1); |
14 | right.setHeight(max(height(right.getLeft()),height(right.getRight()))+1); |
15 | return right; |
16 | } |
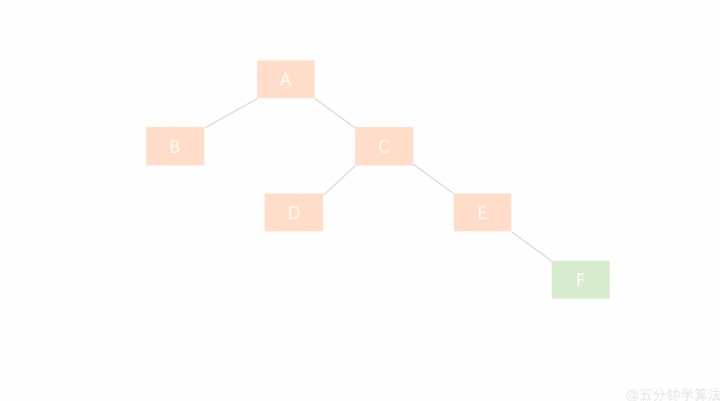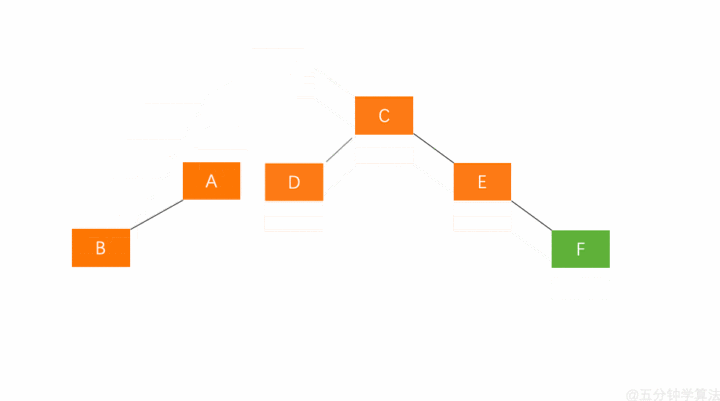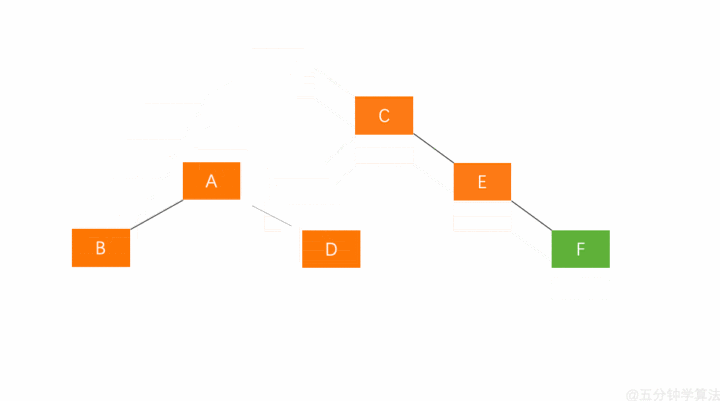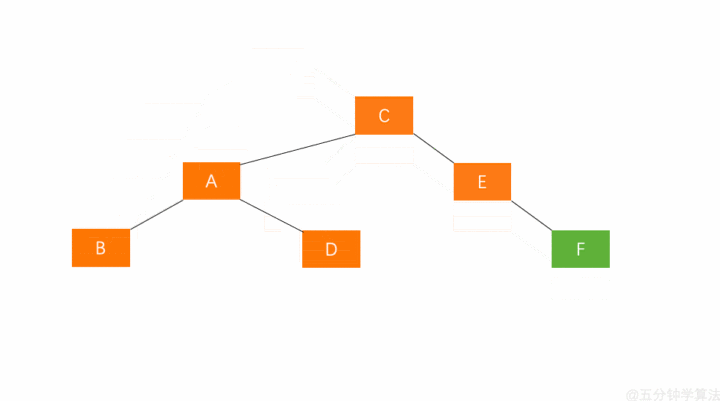
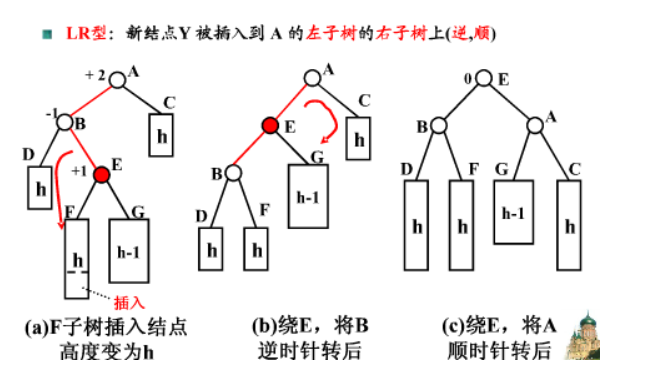
LR型(左孩子的右子树)通过先左旋再右旋解决
若 A 的左孩子节点 B 的右子树 E 插入节点 F ,导致节点 A 失衡
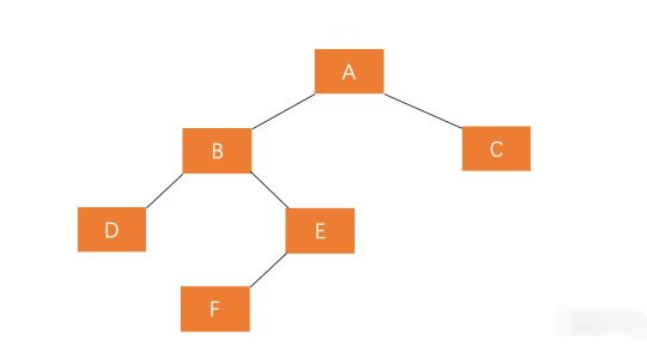
- 解决方案
需要执行两步操作,使得旋转之后为 原来根结点的左孩子的右孩子作为新的根节点,即E作为根节点
- 对失衡节点 A 的左孩子 B 进行左旋操作,即上述 RR 情形操作(左旋)
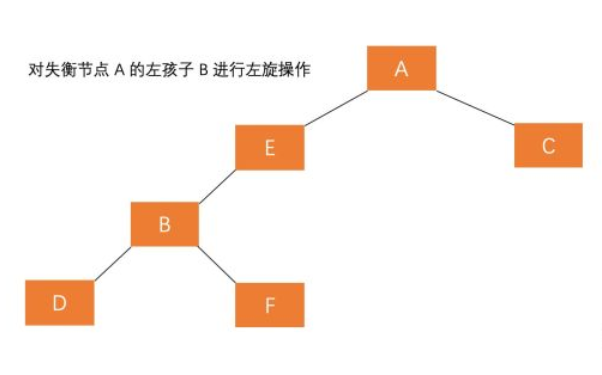
- 对失衡节点 A 做右旋操作,即上述 LL 情形操作(右旋)
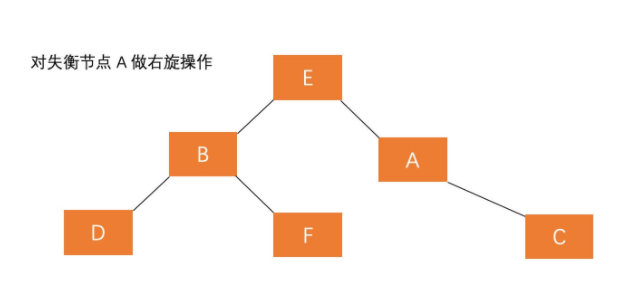
也就是说,经过这两步操作,使得 原来根节点的左孩子的右孩子 E 节点成为了新的根节点。
两次旋转、先左旋后右旋
由于在a的左子树根结点的右子树上插入结点(LR), 导致a的平衡因子由1变成2,导致以a为根结点的子树失去平衡,需要进行两次旋转, 先左旋后右旋
RL型(右孩子的左子树)通过先右旋再左旋解决
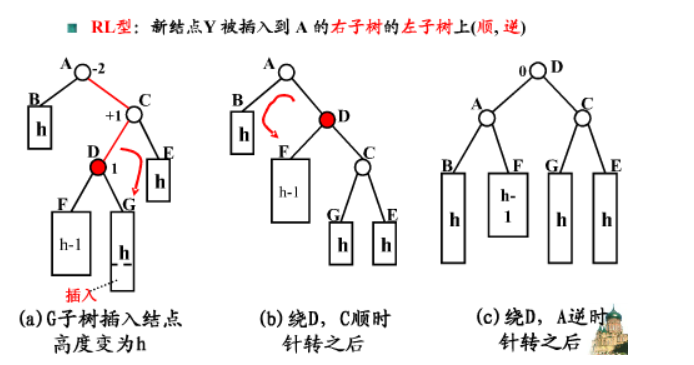
若 A 的右孩子节点 C 的左子树 D 插入节点 F ,导致节点 A 失衡,
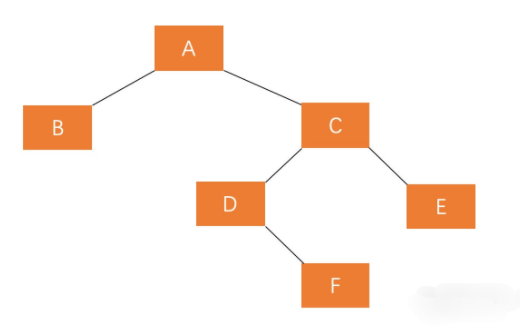
- 解决方案
要执行两步操作,使得旋转之后为 原来根结点的右孩子的左孩子作为新的根节点 。
- 对失衡节点 A 的右孩子 C 进行右旋操作,即上述 LL 情形操作(右旋)
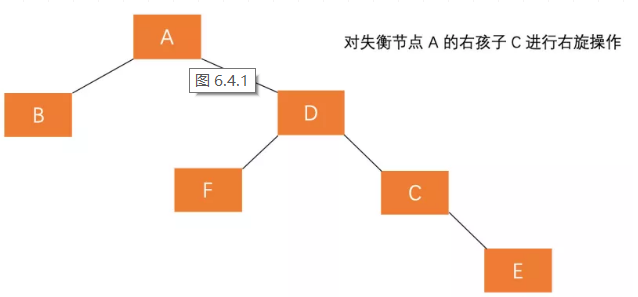
- 对失衡节点 A 做左旋操作,即上述 RR 情形操作(左旋)
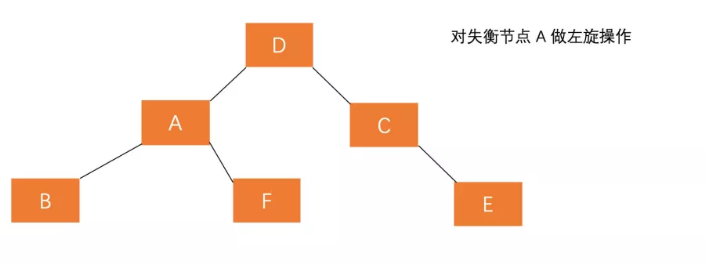
经过这两步操作,使得 原来根节点的右孩子的左孩子 D 节点成为了新的根节点。
两次旋转, 先右旋后左旋
由于在a的右子树根结点的左子树上插入结点(RL), a的平衡因子由-1变成-2,导致以a为根结点的子树失去平衡, 则需要进行两次旋转,先右旋后左旋
总结
- 在所有的不平衡情况中,都是按照先 寻找最小不平衡树,然后 寻找所属的不平衡类别,再 根据 4 种类别进行固定化程序的操作。
- LL , LR ,RR ,RL其实已经为我们提供了最后哪个节点作为新的根指明了方向。如 LR 型最后的根节点为原来的根的左孩子的右孩子,RL 型最后的根节点为原来的根的右孩子的左孩子。只要记住这四种情况,可以很快地推导出所有的情况。
- 维护平衡二叉树,最麻烦的地方在于平衡因子的维护
AVL 树的四种删除节点的方式
VL 树和二叉查找树的删除操作情况一致,都分为四种情况:
- 删除叶子节点
- 删除的节点只有左子树
- 删除的节点只有右子树
- 删除的节点既有左子树又有右子树
AVL 树在删除节点后需要重新检查平衡性并修正,同时,删除操作与插入操作后的平衡修正区别在于,插入操作后只需要对插入栈中的弹出的第一个非平衡节点进行修正,而删除操作需要修正栈中的所有非平衡节点。
删除操作的大致步骤
- 以前三种情况为基础尝试删除节点,并将访问节点入栈。
- 如果尝试删除成功,则依次检查栈顶节点的平衡状态,遇到非平衡节点,即进行旋转平衡,直到栈空。
- 如果尝试删除失败,证明是第四种情况。这时先找到被删除节点的右子树最小节点并删除它,将访问节点继续入栈。
- 再依次检查栈顶节点的平衡状态和修正直到栈空。
对于删除操作造成的非平衡状态的修正,可以这样理解:对左或者右子树的删除操作相当于对右或者左子树的插入操作,然后再对应上插入的四种情况选择相应的旋转就好了。
删除叶子节点
- 将该节点直接从树中删除;
- 其父节点的子树高度的变化将导致父节点平衡因子的变化,通过向上检索并推算其父节点是否失衡;
- 如果其父节点未失衡,则继续向上检索推算其父节点的父节点是否失衡…如此反复2的判断,直到根节点 ;如果向上推算过程中发现了失衡的现象,则进行 4 的处理;
- 如果其父节点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。如果平衡化处理结束后,发现与原来以父节点为根节点的树的高度发生变化,则继续进行 2 的检索推算;如果与原来以父节点为根节点的高度一致时,则可说明父节点的父节点及祖先节点的平衡因子将不会有变化,因此可以退出处理;
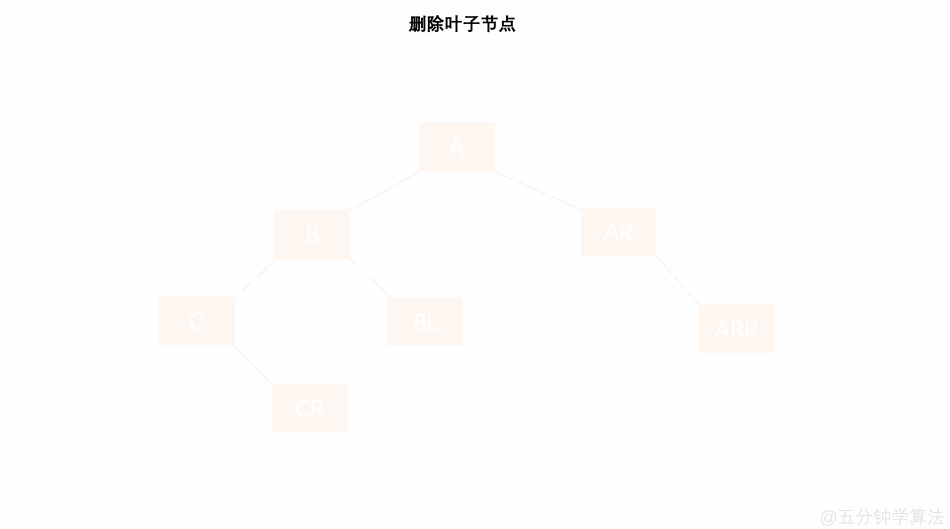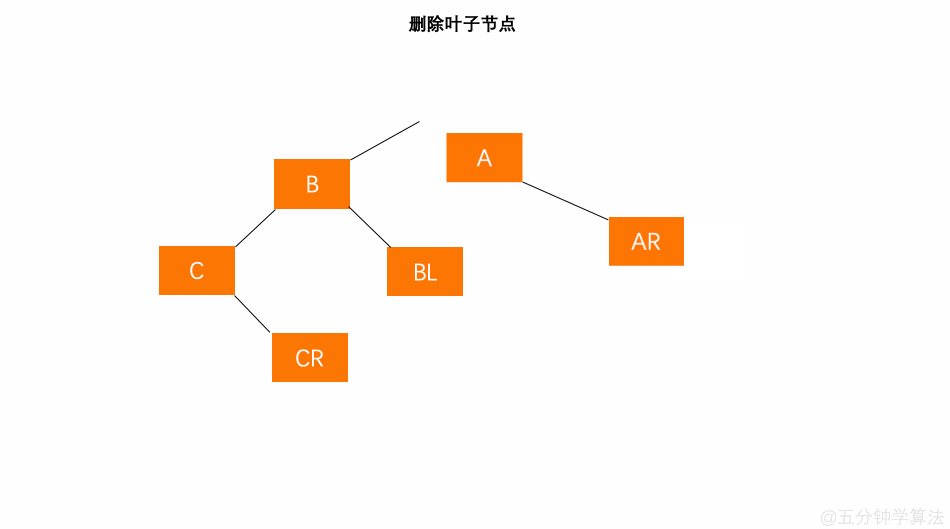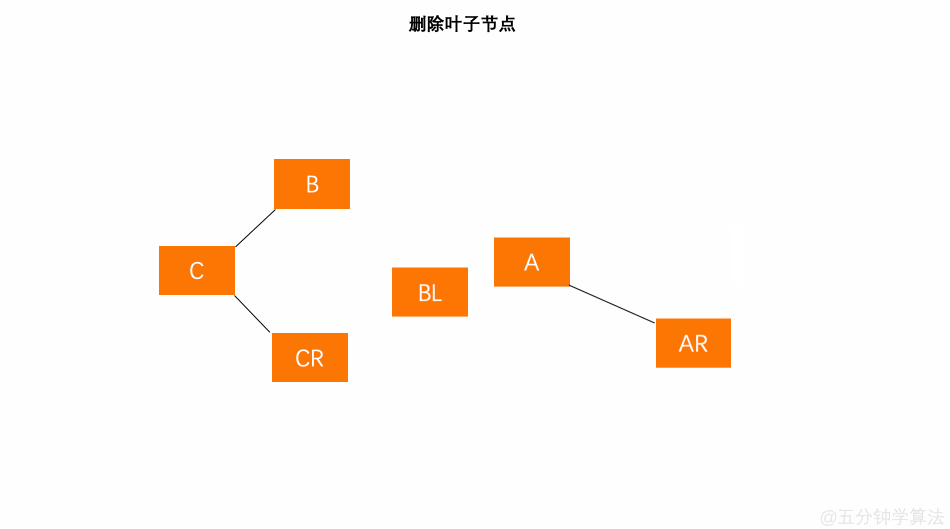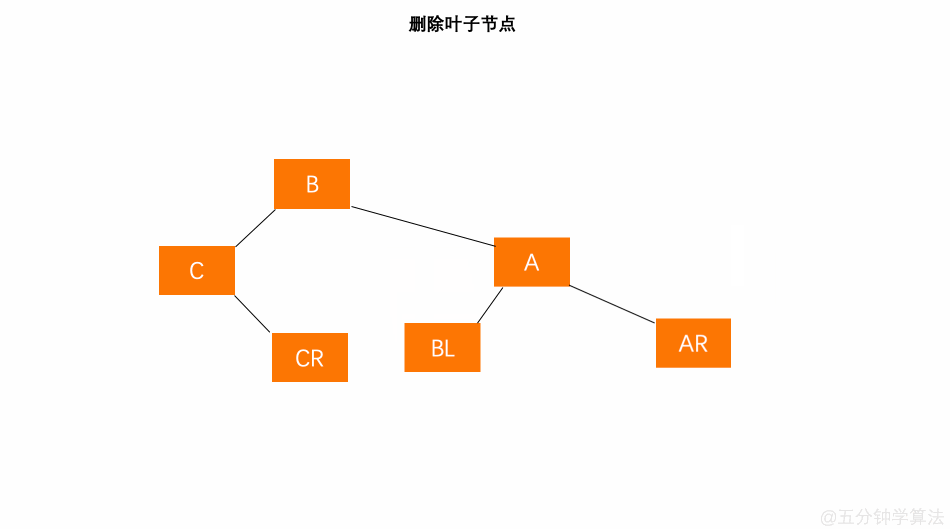
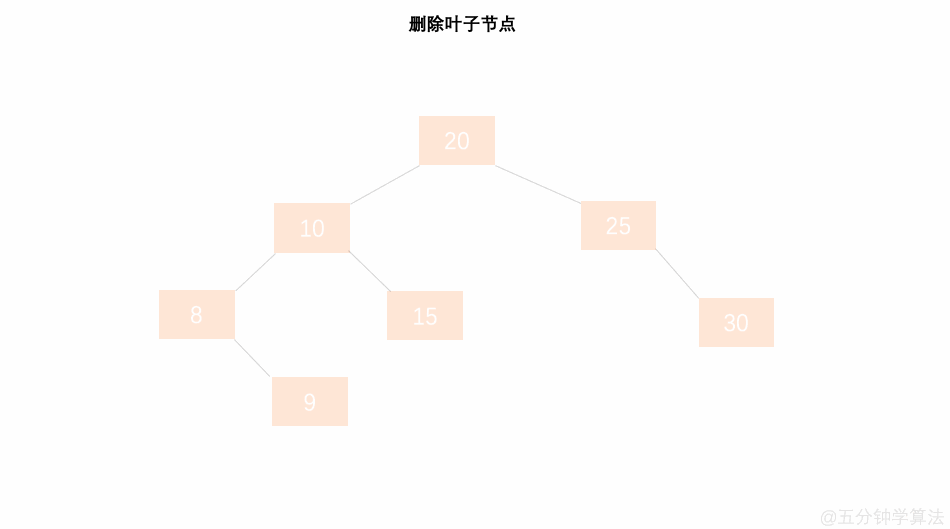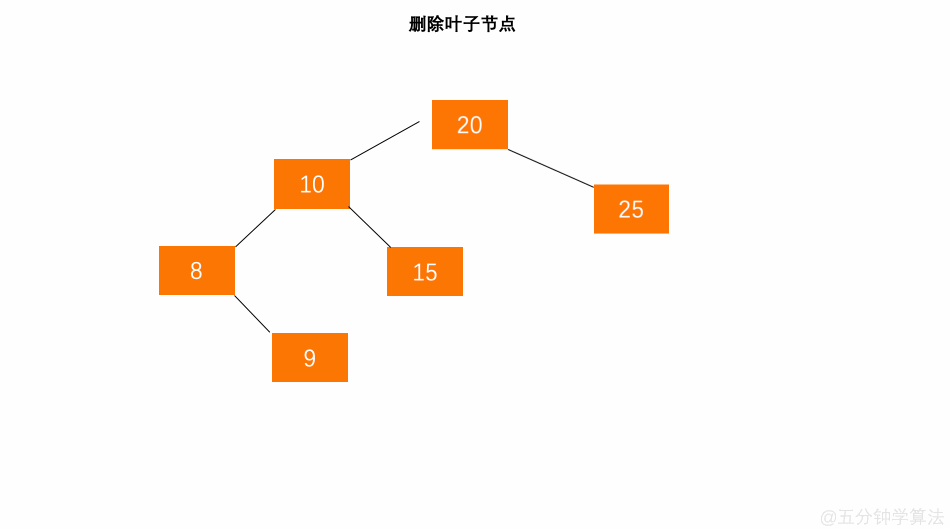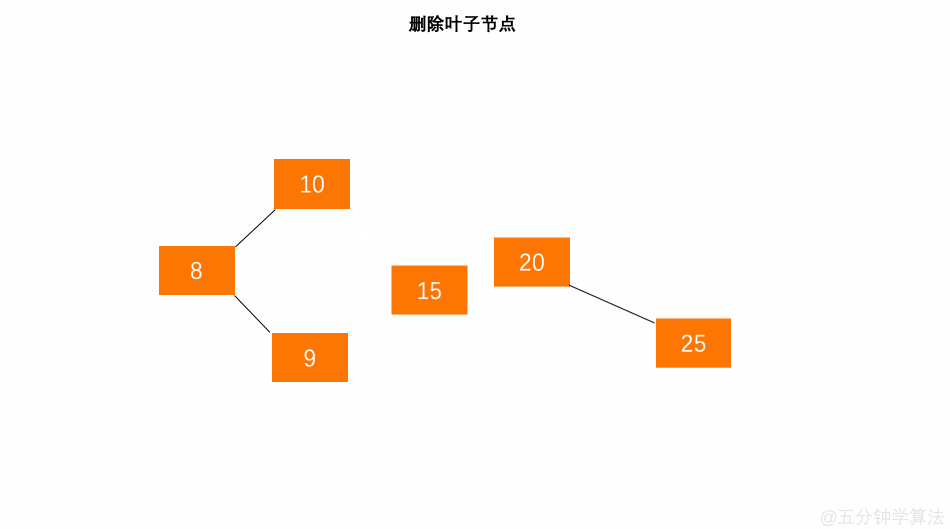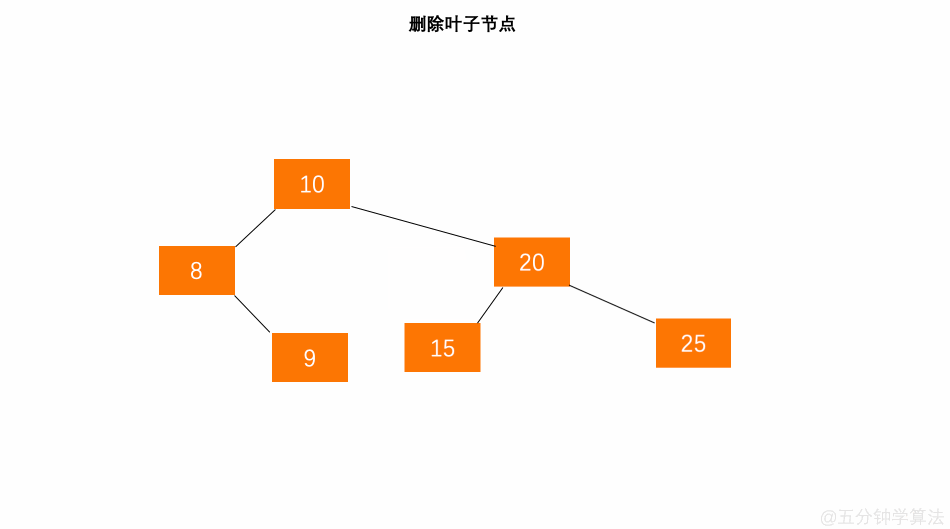
具体数字演示:
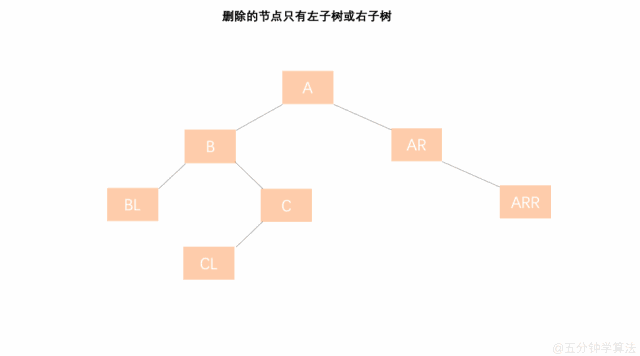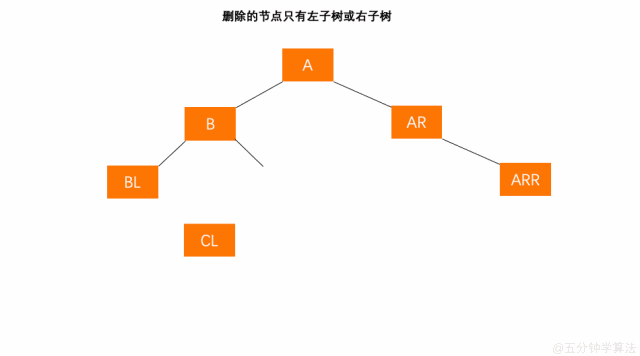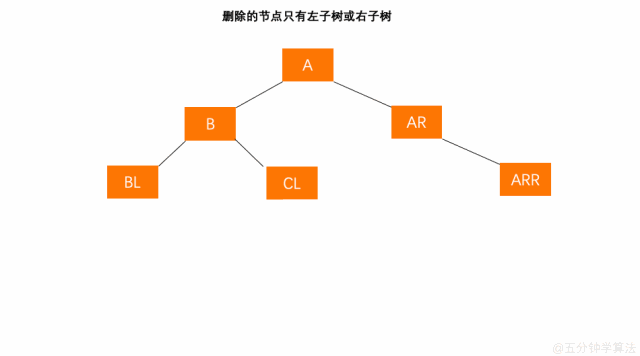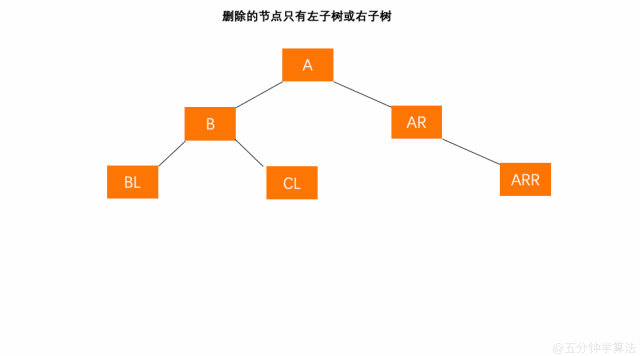
删除的节点只有左子树或右子树
- 将左子树(右子树)替代原有节点 C 的位置;
- 节点 C 被删除后,则以 C 的父节点 B 为起始推算点,依此向上检索推算各节点(父、祖先)是否失衡;
- 如果其父节点未失衡,则继续向上检索推算其父节点 的父节点 是否失衡…如此反复 ② 的判断,直到根节点 ;如果向上推算过程中发现了失衡的现象,则进行 ④ 的处理;
- 如果其父节点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。如果平衡化处理结束后,发现与原来以父节点为根节点的树的高度发生变化,则继续进行 ② 的检索推算;如果与原来以父节点为根节点的高度一致时,则可说明父节点的父节点及祖先节点的平衡因子将不会有变化,因此可以退出处理;
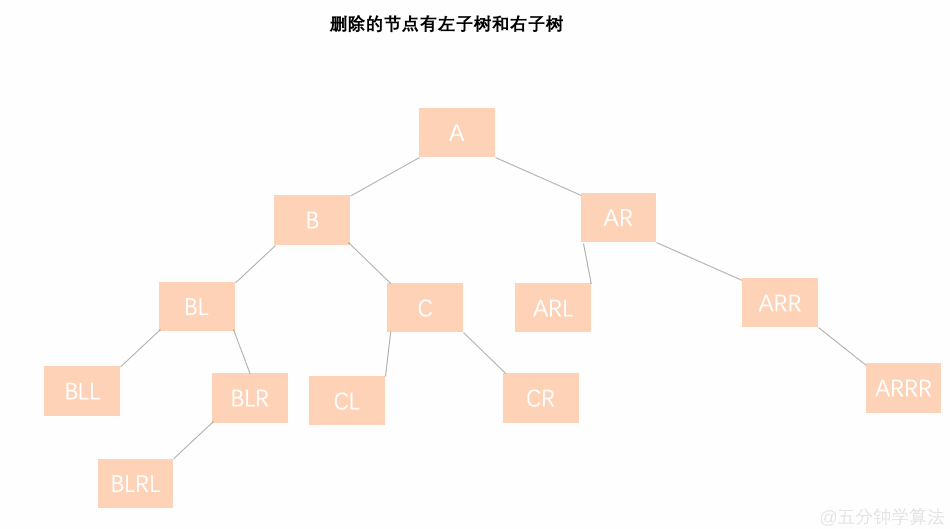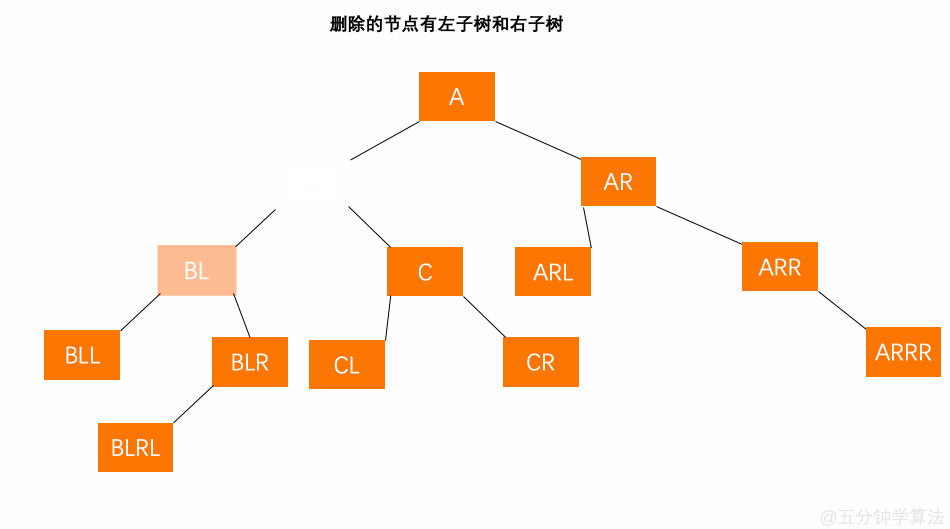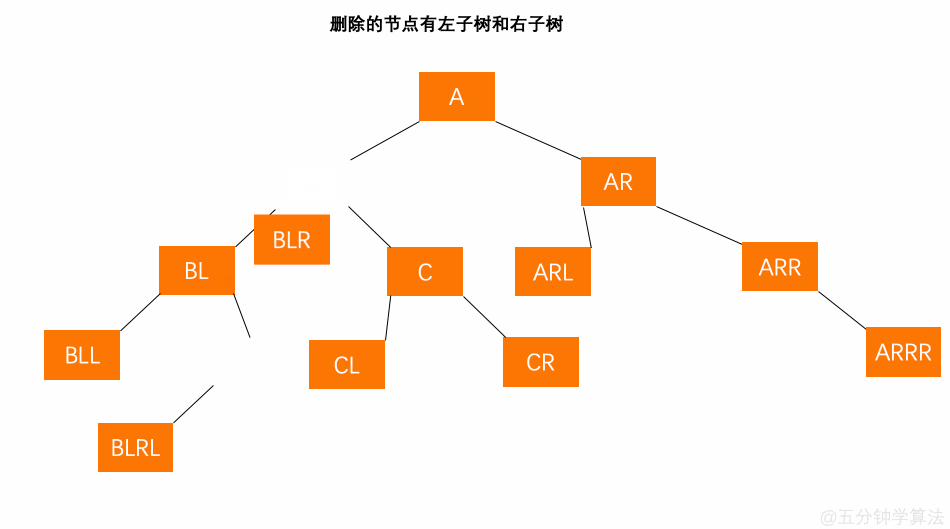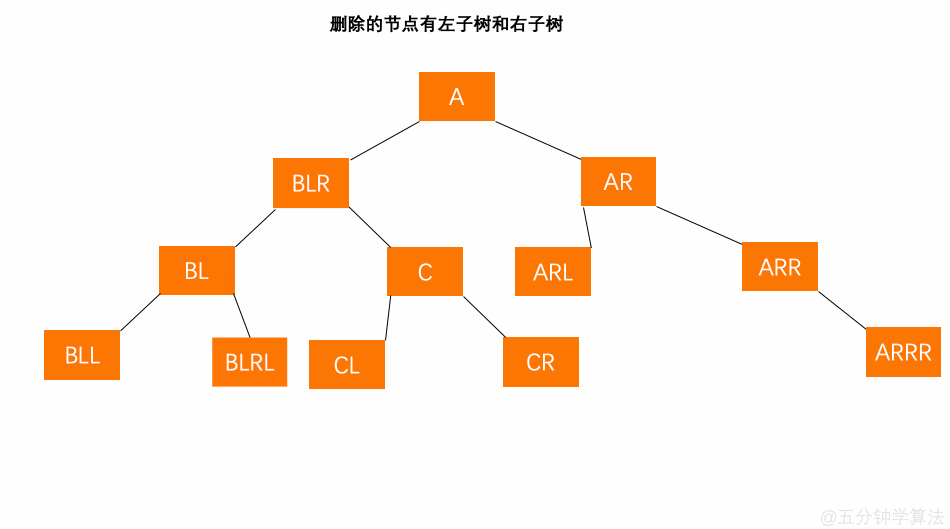
删除的节点既有左子树又有右子树
- 找到被删节点 B 和替代节点 BLR (节点 B 的前继节点或后继节点 —— 在此选择 前继);
- 将替代节点 BLR 的值赋给节点 B ,再把替代节点 BLR 的左孩子 BLRL 替换替代节点 BLR 的位置;
- 以 BLR 的父节点 BL 为起始推算点,依此向上检索推算父节点或祖先节点是否失衡;
- 如果其父节点未失衡,则继续向上检索推算其父节点的父节点是否失衡…如此反复③的判断,直到根节点;如果向上推算过程中发现了失衡的现象,则进行⑤的处理;
- 如果其父节点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。如果平衡化处理结束后,发现与原来以父节点为根节点的树的高度发生变化,则继续进行 ② 的检索推算;如果与原来以父节点为根节点的高度一致时,则可说明父节点的父节点及祖先节点的平衡因子将不会有变化,因此可以退出处理;