al_04 BinarySearchTree


阅读数: 次   
如需转载，请根据 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 许可，附上本文作者及链接。
本文作者： 执笔成念
作者昵称： zbcn
本文链接： https://1363653611.github.io/zbcn.github.io/2020/06/20/al_04_BinarySearchTree/

树

树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根。

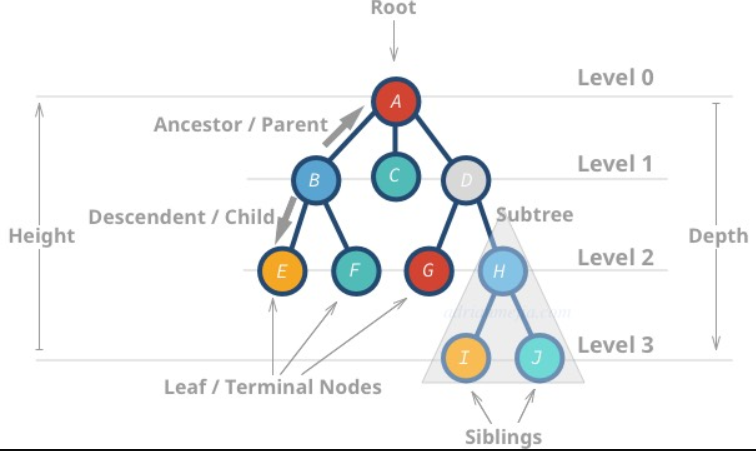
image-20200817155853997

树的相关概念

根节点 Root node

没有任何父节点的节点：最顶层的节点被称为根（root）节点

叶子节点 leaf node

没有任何子节点的节点被称为叶子节点（leaf node）或者终端节点（terminal node）。

树的高度 Height

最深的叶节点与根节点之间的距离（即边的数量）

  • 以A为根节点的树 的高度是 3。
  • 以I为根节点的树 的高度是 0（子树也是树，I 的度是指 I 为根节点的子树的度）。

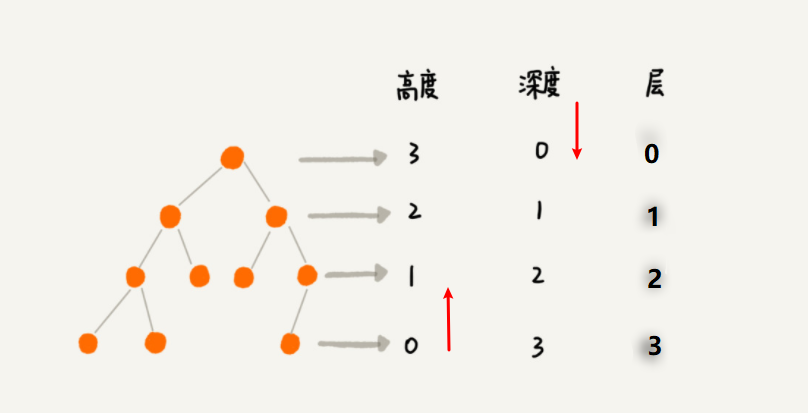
树的深度 Depth

深度（Depth）或者层次（level）是节点与根节点的距离。

  • H 的层次是 2。
  • B 的层次是 1。

深度定义是从上往下的，高度定义是从下往上的

image-20200819113604884

二叉树 Binary Tree

二叉树(binary)是一种特殊的树，它是每个节点最多有两个子树的树结构，通常子树被称作是 “左子树” 和 “右子树”，二叉树常用于实现二叉搜索树和二叉堆。

image-20200817162341501

常见的二叉树：完全二叉树,满二叉数,二叉搜索数,二叉堆,AVL 树,红黑树，哈夫曼树

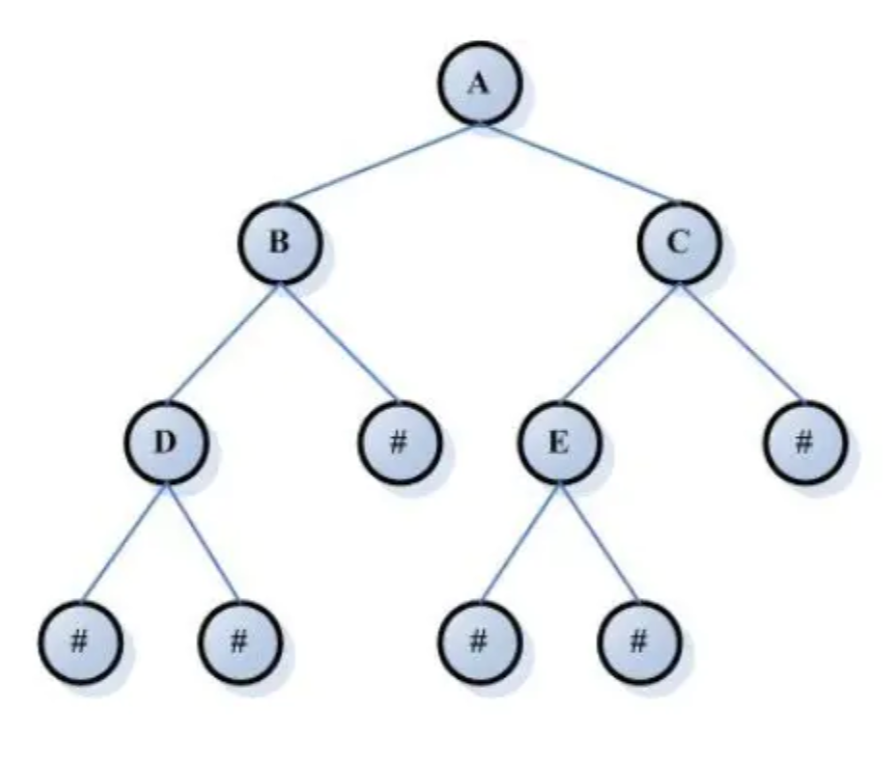
完全二叉树 Complete Binary Tree

若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

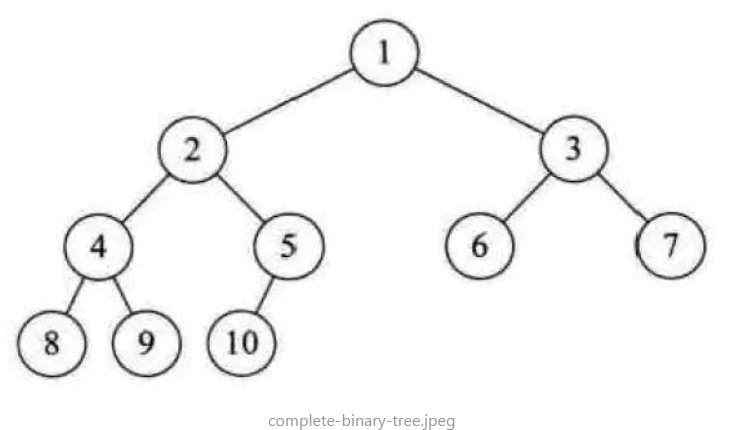
image-20200817162901507

即除了最后一层外，每一层上的节点数均达到最大值；在最后一层上只缺少右边的若干结点。

而像这样就不是完全二叉树, 例如下图：(# 代表有元素)

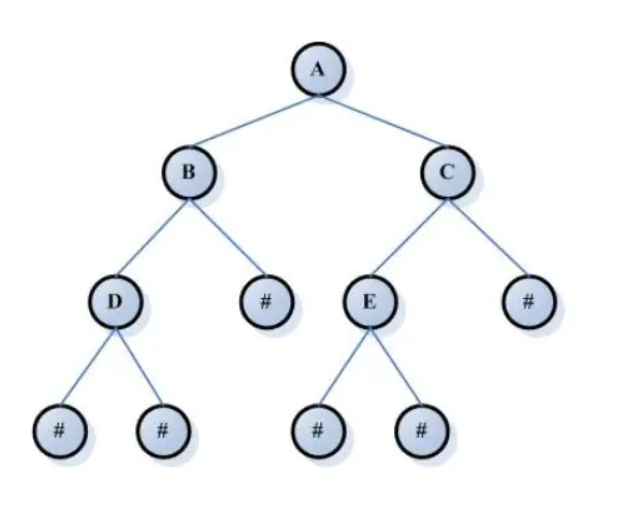
image-20200817163136382

用途：

完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高。后面介绍的二叉堆也是基于完全二叉树来实现的。

满二叉树 Full Binary Tree

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树被称之为满二叉树。

满二叉树一定是完全二叉树，完全二叉树不一定满二叉树。

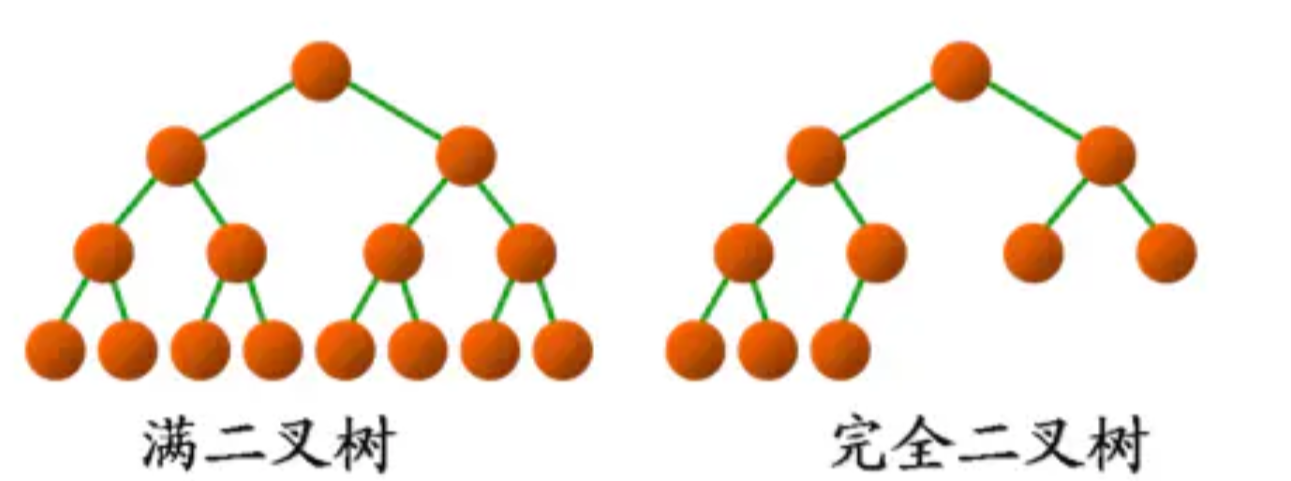
image-20200817163554327

一个高度为 h 的满二叉树含有 1 + 2 + 4 + ... + 2^h = 2^(h + 1) - 1个节点，所以满二叉树的节点个数一定为奇数。

二叉搜索树 (Binary Search Tree)

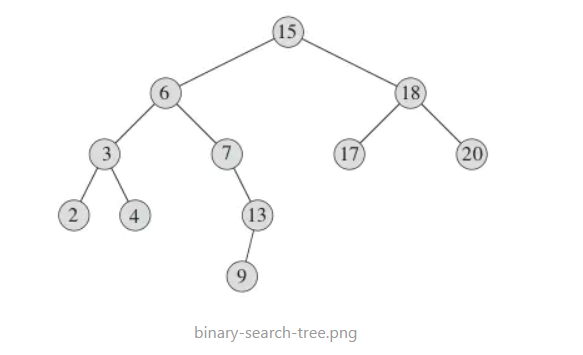
二叉搜索树是一种特殊的二叉树，也可以称为二叉排序树，二叉查找树。除了具有二叉树的基本性质外，它还具备：

  • 树中每个节点最多有两个子树，通常称为左子树和右子树
  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
  • 它的左右子树仍然是一棵二叉搜索树 (recursive)

image-20200817164428643

基本操作

数据结构

1
class TreeNode<E extends Comparable<E>>{
2
    private E data;
3
    private TreeNode<E> left;
4
    private TreeNode<E> right;
5
    private TreeNode<E> parent;
6
    TreeNode(E theData){
7
        data = theData;
8
        left = null;
9
        right = null;
10
        parent = null;
11
    }
12
}
13
public class BinarySearchTree<E extends Comparable<E>>{
14
    private TreeNode<E> root = null;
15
}

树的遍历

假设我们需要遍历树中所有节点，这里有许多递归方法可以实现：(中序,前序,后序 指的是 父节点遍历的位置)

中序遍历

当到达某个节点时，先访问左子节点，再输出该节点，最后访问右子节点。

1
public void inOrder(TreeNode<E> cursor){
2
    if(cursor == null) return;
3
    inOrder(cursor.getLeft());
4
    System.out.println(cursor.getData());
5
    inOrder(cursor.getRight());
6
}

前序遍历

前序遍历：当到达某个节点时，先输出该节点，再访问左子节点，最后访问右子节点。

1
public void preOrder(TreeNode<E> cursor){
2
    if(cursor == null) return;
3
    System.out.println(cursor.getData());
4
    inOrder(cursor.getLeft());
5
    inOrder(cursor.getRight());
6
}

后续遍历

当到达某个节点时，先访问左子节点，再访问右子节点，最后输出该节点。

1
public void postOrder(TreeNode<E> cursor){
2
    if(cursor == null) return;
3
    inOrder(cursor.getLeft());
4
    inOrder(cursor.getRight());
5
    System.out.println(cursor.getData());
6
}

树的搜索

树的搜索和树的遍历差不多，就是在遍历的时候只搜索不输出就可以了:

example:我们在树中搜索元素 20

img

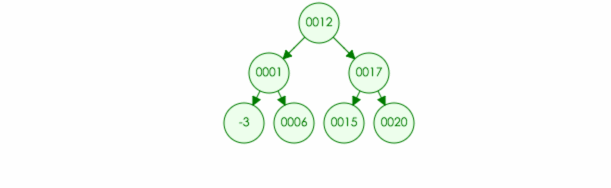
代码实现:

1
	/**
2
     * 非递归方式查找
3
     * @param currentNode
4
     * @param data
5
     * @return
6
     */
7
public boolean searchNode(TreeNode<E> node){
8
    TreeNode<E> currentNode = root;
9
    while(true){
10
        if(currentNode == null){
11
            return false;
12
        }
13
        if(currentNode.getData().compareTo(node.getData()) == 0){
14
            return true;
15
        }else if(currentNode.getData().compareTo(node.getData()) < 0){
16
            currentNode = currentNode.getLeft();
17
        }else{
18
            currentNode = currentNode.getRight();
19
        }
20
    }
21
}
22
23
    /**
24
     * 查找的递归版本
25
     * @param currentNode
26
     * @param data
27
     * @return
28
     */
29
    public TreeNode<E> search2(TreeNode<E> currentNode,E data){
30
        if (Objects.isNull(currentNode)){
31
            return null;
32
        }
33
        if(currentNode.getData().compareTo(data) < 0){
34
           return search2(currentNode.getRight(),data);
35
        }else if(currentNode.getData().compareTo(data) > 0){
36
            return search2(currentNode.getLeft(),data);
37
        }else{
38
            //currentNode.getData().compareTo(data) == 0
39
            return currentNode;
40
        }
41
    }

前驱和后驱节点

二叉树的节点val值是按照二叉树中序遍历顺序连续设定

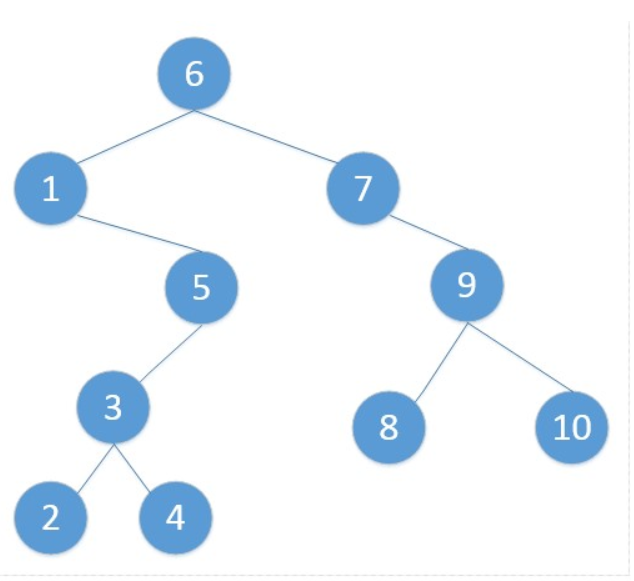
image-20200818133923792

节点的前驱节点

节点val值小于该节点val值并且值最大的节点

找结点(x)的前驱结点。即，查找”二叉树中数据值小于该结点”的”最大结点”。

上图的结果:

  • 4的前驱结点是3
  • 2的前驱结点是1
  • 6的前驱结点是5

寻找前驱节点的方法论:

  1. 若一个节点有左子树，那么该节点的前驱节点是其左子树中val值最大的节点（也就是左子树中所谓的rightMostNode）
  2. 若一个节点没有左子树，那么判断该节点和其父节点的关系
    2.1 若该节点是其父节点的右边孩子，那么该节点的前驱结点即为其父节点。
    2.2 若该节点是其父节点的左边孩子，那么需要沿着其父亲节点一直向树的顶端寻找，直到找到一个节点P，P节点是其父节点Q的右边孩子（可参考例子2的前驱结点是1），那么Q就是该节点的后继节点

代码实现

1
/**
2
  * 前驱节点
3
  * 找结点(x)的前驱结点。即，查找"二叉树中数据值小于该结点"的"最大结点"。
4
  * @param node
5
  * @return
6
  */
7
 public TreeNode<E> predecessor(TreeNode<E> node){
8
     //若该节点有左子节点,则前驱节点为"以其左孩子为根的子树的最大结点"。
9
     if(node.getLeft() != null){
10
         return getMaxNode(node.getLeft());
11
     }
12
13
     //若该节点不存在左子节点:
14
     //1. 该节点为其父节点的右子节点,则"node的前驱结点"为 "它的父结点"
15
     //2. 该节点为其父节点的左子节点,则查找"node的最低的父结点，并且该父结点要具有右孩子"，找到的这个"最低的父结点"就是"x的前驱结点"
16
     //寻找其父辈节点中,左子树为null 的第一个父辈节点
17
     TreeNode<E> parent = node.getParent();
18
     // //node != parent.getLeft() 时,说明 node 就是 parent 的右子节点
19
     while (parent!= null && node == parent.getLeft()){
20
         node = parent;
21
           parent = parent.getParent();
22
     }
23
     return parent;
24
 }

节点的后继节点

节点val值大于该节点val值并且值最小的节点

找结点(x)的后继结点。即，查找”二叉树中数据值大于该结点”的”最小结点”。

上图结果:

  • 7的后继结点是8
  • 5的后继节点是6
  • 2的后继节点是3

寻找后继结点的方法论

  1. 若一个节点有右子树，那么该节点的后继节点是其右子树中val值最小的节点（也就是右子树中所谓的leftMostNode）
  2. 若一个节点没有右子树，那么判断该节点和其父节点的关系
    2.1 若该节点是其父节点的左边孩子，那么该节点的后继结点即为其父节点
    2.2 若该节点是其父节点的右边孩子，那么需要沿着其父亲节点一直向树的顶端寻找，直到找到一个节点P，P节点是其父节点Q的左边孩子（可参考例子5的后继节点是6），那么Q就是该节点的后继节点

代码实现

1
/**
2
     * 后继节点
3
     * 找结点(x)的后继结点。即，查找"二叉树中数据值大于该结点"的"最小结点"。
4
     * @param node
5
     * @return
6
     */
7
    public TreeNode<E> successor(TreeNode<E> node){
8
        //1. 如果该节点有右侧节点,则后继结点"为 "以其右孩子为根的子树的最小结点"。
9
        if(node.getRight() != null){
10
            return getMinNode(node.getRight());
11
        }
12
        //如果改节点不存啊在右侧节点
13
        //1. 该节点为其父节点的左侧节点,则"node的后继结点"为 "它的父结点"
14
        //2. 该节点为其父节点的右侧节点,则查找"node的最低的父结点，并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。
15
        TreeNode<E> parent = node.getParent();
16
        //node != parent.getRight() 时,说明 node 就是 parent 的左子节点
17
        while (parent!=null && node == parent.getRight()){
18
            node = parent;
19
            parent = parent.getParent();
20
        }
21
        return parent;
22
    }

参考:https://www.cnblogs.com/xiejunzhao/p/f5f362c1a89da1663850df9fc4b80214.html

节点插入

步骤：

  1. 递归地去查找该二叉树，找到应该插入的节点
  2. 若当前的二叉查找树为空，则插入的元素为根节点
  3. 若插入的元素值小于根节点值，则将元素插入到左子树中
  4. 若插入的元素值不小于根节点值，则将元素插入到右子树中

比如：我们往树种插入元素 21

img

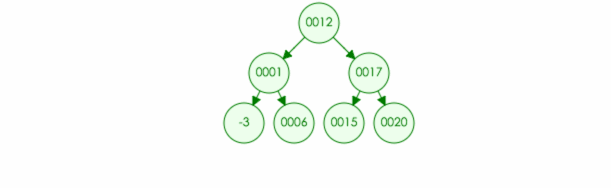
代码实现：

1
public void insertNode(TreeNode<E> node){
2
    TreeNode<E> currentNode = root;
3
    if(currentNode == null){
4
        root = node;
5
        return;
6
    }else{
7
        while(true){
8
            if(node.getData().compareTo(currentNode.getData()) < 0){
9
                if(currentNode.getLeft() == null){
10
                    break;
11
                }else{
12
                    currentNode = currentNode.getLeft();
13
                }
14
            }else if(node.getData().compareTo(currentNode.getData()) > 0){
15
16
                if(currentNode.getRight() == null){
17
                    break;
18
                }else{
19
                    currentNode = currentNode.getRight();
20
                }
21
            }
22
        }   
23
    }
24
    if(node.getData().compareTo(currentNode.getData()) < 0){
25
        currentNode.setLeft(node);
26
    }else if(node.getData().compareTo(currentNode.getData()) > 0){
27
        currentNode.setRight(node);
28
    }
29
}

节点删除：

首先需要搜索该节点，然后可以分为以下四种情况进行讨论：

  1. 如果找不到该节点，那么什么都不用做

例如：要在树中删除元素 22

img

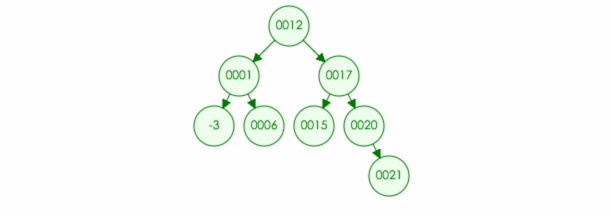
  1. 如果被移除的元素在叶节点(no children)：那么直接移除该节点，并且将父节点原本指向该位置改为 null (如果是根节点，那就不用修改父节点指向位置)

例如：要在树中删除元素 6

img

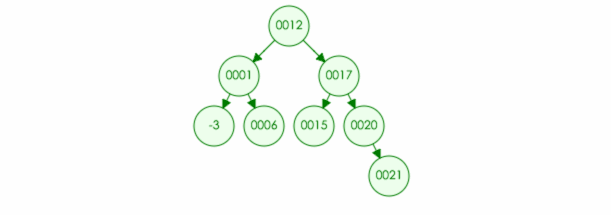
  1. 如果删除的元素只有一个儿子(one child)：那么也很简单，直接删除该节点，并且将父节点原本指向的位置改为该儿子 (如果是根节点，那么该儿子成为新的根节点)

例如：要在树中删除元素 20

img

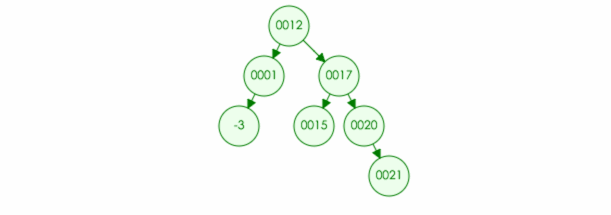
  1. 如果删除的元素有两个儿子，那么可以取左子树中最大元素(前驱节点)或者右子树中最小元素(后继节点)进行替换，然后将最大元素最小元素原位置置空

例如：要在树中删除元素 15

img

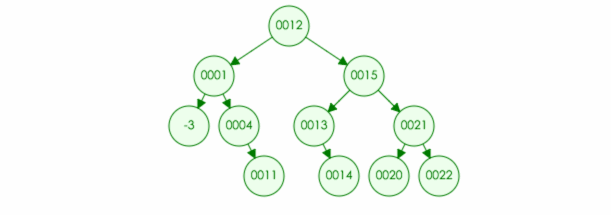
源码实现

1
public TreeNode<E> remove(TreeNode<E> node){
2
        // node 节点的左右子树都不为null
3
        if(node.getRight() != null && node.getLeft() != null){
4
            //找到后继节点
5
            TreeNode<E> successor = successor(node);
6
            //转移后继结点值到当前节点
7
            node.setData(successor.getData());
8
            //把要删除的当前节点设置为后继结点
9
            node = successor;
10
        }
11
        //只有一个子节点,或者没有子节点
12
        TreeNode<E> child = null;
13
        if(node.getLeft() != null){
14
            child = node.getLeft();
15
        }else{
16
            child = node.getRight();
17
        }
18
        //如果 child != null，就说明是有一个节点的情况
19
        if(child != null){
20
            //将子节点和父节点关联上
21
            child.setParent(node.getParent());
22
        }
23
        //如果当前节点没有父节点（后继情况到这儿时一定有父节点）
24
        //说明要删除的就是根节点
25
        TreeNode<E> parent = node.getParent();
26
        if( parent == null){
27
            //根节点设置为子节点
28
            //按照前面逻辑，根只有一个或者没有节点，所以直接赋值 child 即可
29
            root = child;
30
        }else if(node == parent.getLeft()){ //子节点时父亲的做左节点
31
            //将父节点的左节点设置为 child
32
            parent.setLeft(child);
33
        }else{//子节点时父亲的右子节点
34
            parent.setRight(child);
35
        }
36
        return node;
37
    }

平衡树 Balanced Tree：

平衡树的应用

  1. 排序：我们可以将数据一个个读取，构造出一棵平衡树。但我们读取完所有数据后，我们可以按次序遍历该树。但是在插入的过程中需要不断调整。否则他有可能会越来与不平衡，调整的方式有我们后面介绍的 AVL 树和红黑树两种方法。
  2. 时间复杂度为 O(nlog2n + n)
  3. 编译算数表达式：
    我们可以将算术表达式展现为一棵搜索树：所有的叶子节点都是常量或者变量，而除叶节点外所有节点都是操作符。

比如：我们可以将 (A + B) * (C + D) * 2 - X / Y展现为:

img

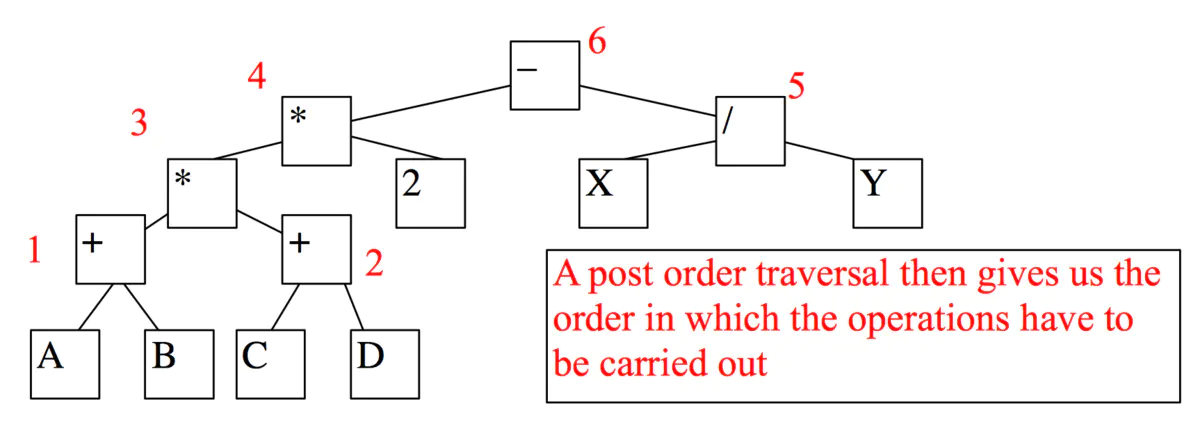
平衡树分析

二叉搜索树虽然在插入和删除时的效率都有所提升，但是如果二叉树变成了下图：

img

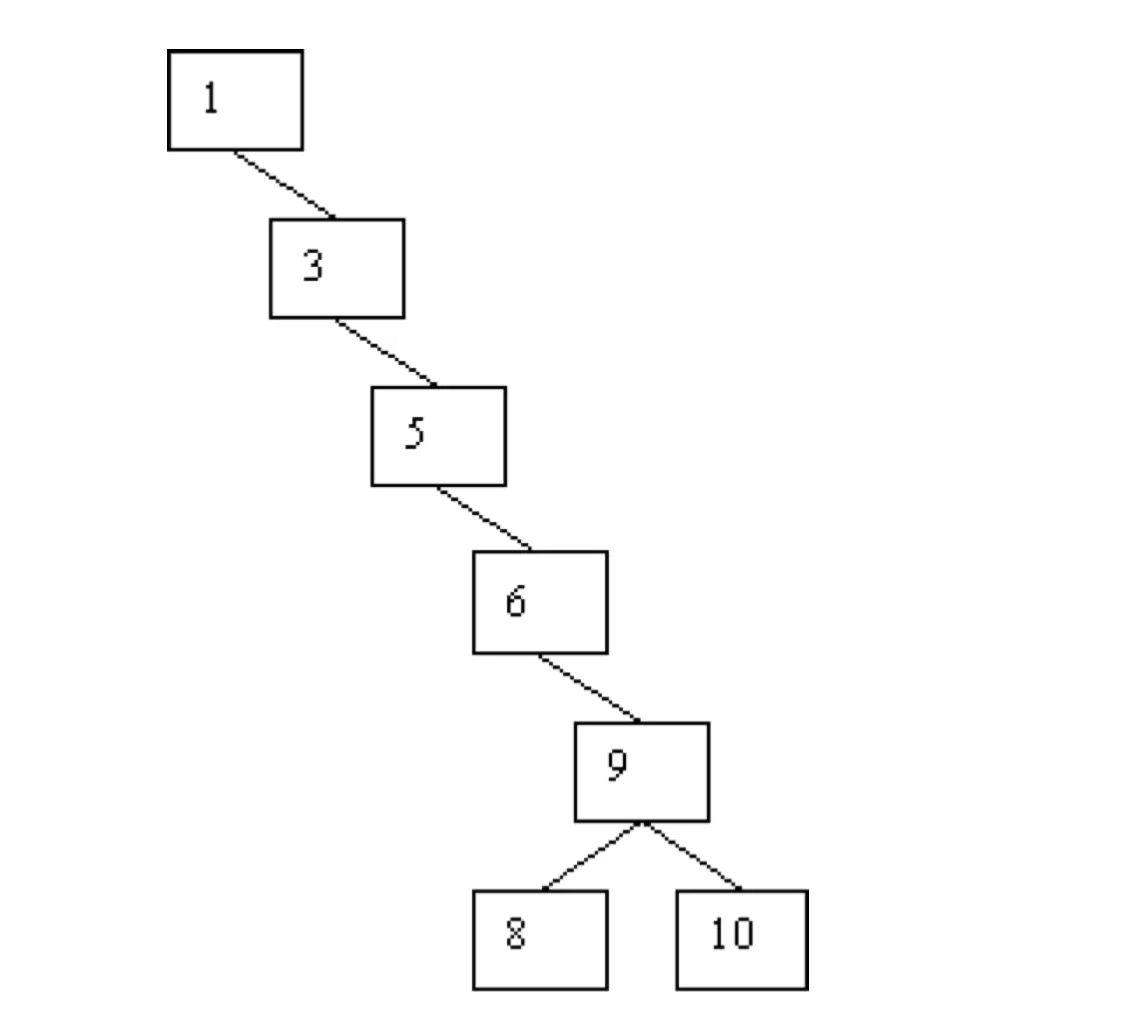
二叉树快退化成了，那么搜索效率效率就会变得很低,时间复杂度由 logn 退化到 n，这时候我们需要添加一些额外的条件来约束它，使其可以保持具有 log(n) 的时间复杂度。

  • 首先平衡树得是二叉树，它满足二叉树的所有性质。
  • 判定是否为平衡树的条件：将该树重新排序，若不存在重新排序后的二叉树的树高比原来的树小，则判定该树为平衡树。

比如:

img

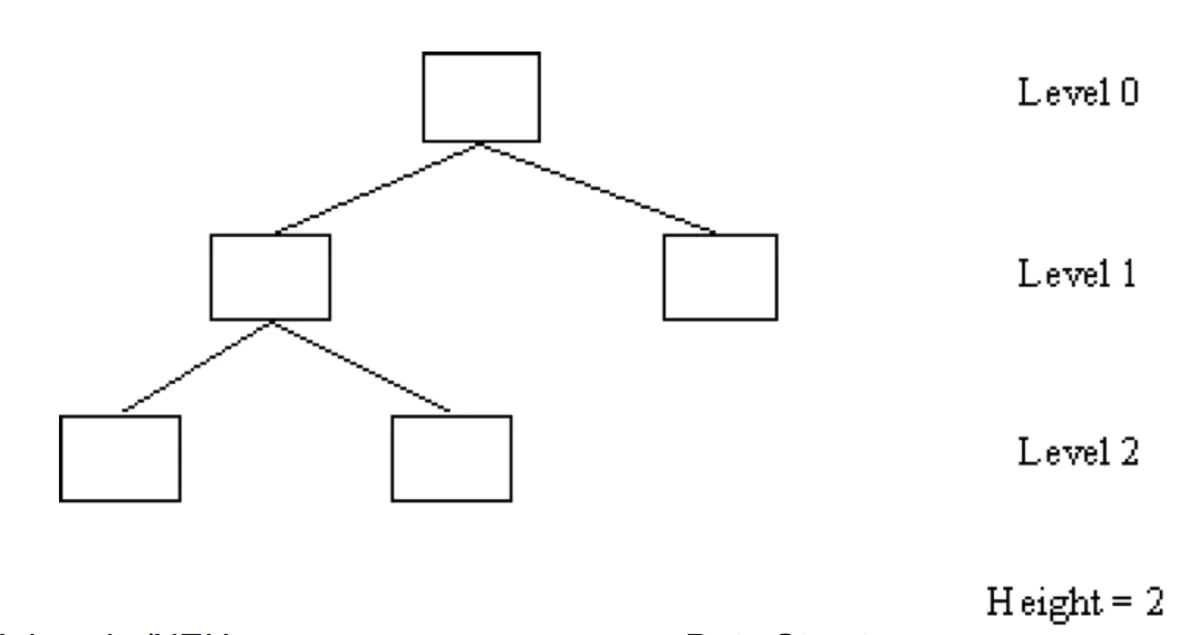
这里有棵树高度为 2，那么我们知道高度为 1 的树最多只有三个节点，五个节点是无法构成一棵高度为 1 的二叉树，故上图的二叉树是平衡树。

又比如:

img

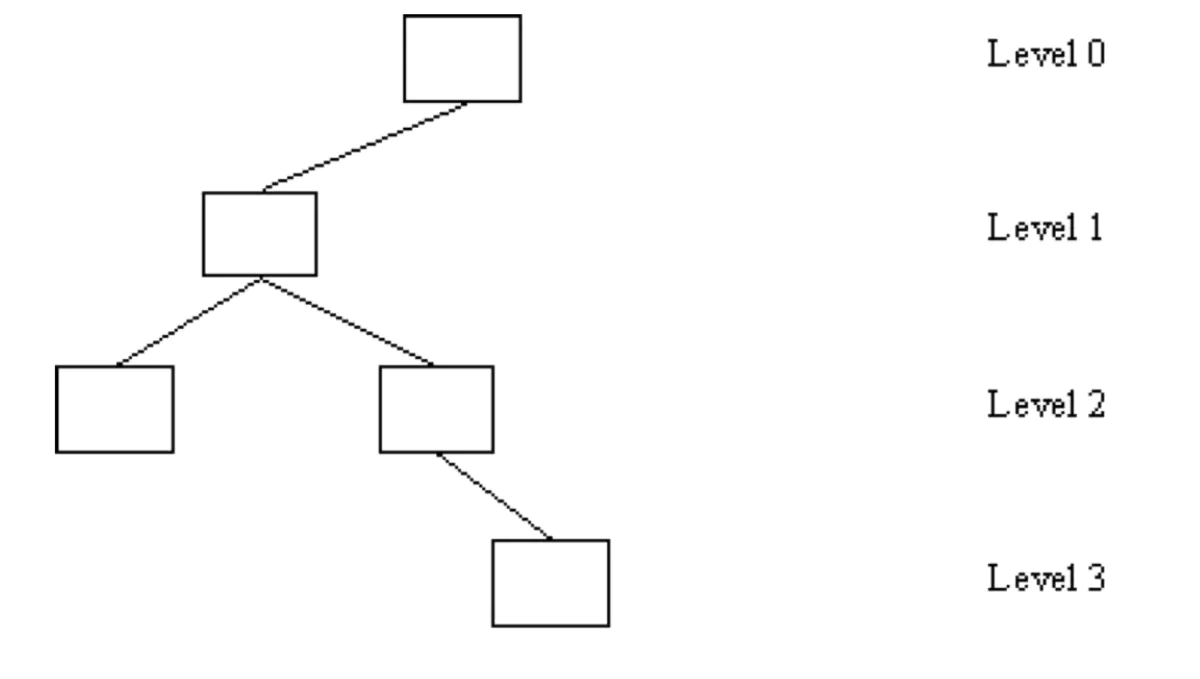
该树高度为 3，我们知道一棵高度为 2 的树最多可以有 2^(h + 1) - 1 = 7(满二叉树)的节点，故图上的的树只有五个节点，那么它经过重新调整之后可以变为一个高度为 2 的二叉树，故不符合平衡树的性质，故该树不是平衡树。

由上我们可以得出一个结论：

  1. 如果一棵树是平衡的，那么它所满足的节点数 n 需要满足 2^h - 1 < n <= 2^(h + 1) - 1
  2. 插入和删除一个节点的时间复杂度均为: O(logn)
  3. 这里虽然有一些算法可以使平衡二叉树 - 但是它们并没什么卵用，因为我们一般都是在添加或删除操作时候来去平衡树，而不是再一开始去平衡树
赏

谢谢你请我吃糖果

支付宝
微信

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

身在井隅<br><br> 心想星光<br><br> 眼里有诗<br><br>自在远方